Comparison with the old method

In this section the centrality cut method described in this note and the Get_centrality function³ are investigated.

It is fairly simple to check if, say a 10 percent centrality cut really corresponds to the 10 percent of events with the highest multiplicity. From a sample of $N$ minimum bias event the cut should give $N/10$ events -- in other words $N_{10\%}/N = 0.10$.

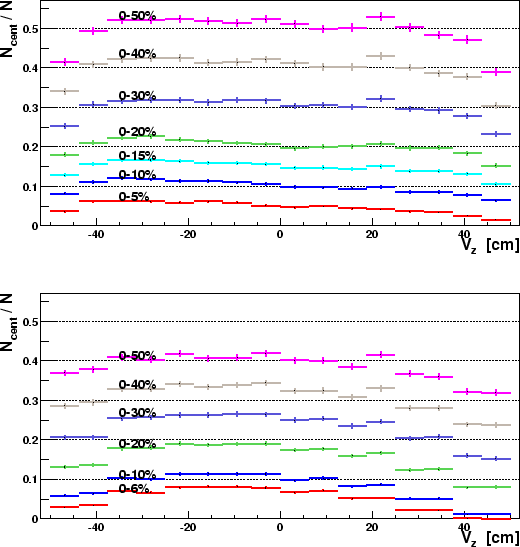
Approximately 400,000 minimum bias events (i.e. inclusive trigger 4 with at least one hit in the tiles) from run 2481 have been analysed. For 16 vertex bins the ratio $N_{cent}/N$ has been found for the different (inclusive) centrality cuts in the two methods. Figures 5 and 6 (blow-up) show the results.

Figure 5: $N_{cent}/N$ from BrTileCentModule, based on fitted cut values in $M$ (top), from Get_centrality, based on constant cut values in $M$ (bottom)

Figure 6: Same as figure 5, but only up to 20%, to emphasise the change from Get_centrality (bottom) to BrTileCentModule (top).

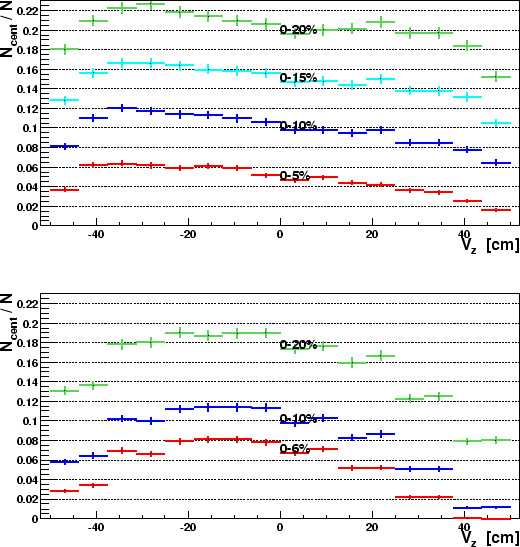It's clear from the figures that the centrality cuts are improved, but they are still not perfect. It seems that there is some systematic effect on the edge bins, which means that the centrality of events with $\vert V_z\vert >$ 40cm is still overestimated. The $N_{cent}/N$ ratio for the 5%, 10% and 15% cuts shows a systematic decrease for growing $V_z$. We believe that these effects are due to the improper $S$ fits. We will systematically investigate the fitting, and try to come up with a better calibration.